Posted At: Feb 28, 2025 - 108 Views
Introduction
Sorting is a fundamental operation in computer science, widely used in data processing, searching algorithms, and optimization problems. In this project, we implement and analyze two classic sorting algorithms:
🔹 Modified Bubble Sort – An optimized version that reduces unnecessary iterations.
🔹 Selection Sort with Reverse Order Support – A modified version that sorts in both ascending and descending order.
This study explores the efficiency, time complexity, and practical applications of these algorithms, comparing them with insertion sort for partially sorted data.
🚀 Download the Full Code (Python): Click Here
1. Understanding the Modified Bubble Sort Algorithm
📌 Key Insight: Bubble sort is inefficient for large datasets but can be optimized by reducing unnecessary swaps.
🔹 Code Implementation (Python):
def modified_bubble_sort(arr):
n = len(arr)
for i in range(n):
swapped = False
for j in range(0, n-i-1):
if arr[j] > arr[j+1]:
arr[j], arr[j+1] = arr[j+1], arr[j]
swapped = True
if not swapped:
break
return arr
# Testing with a random list
import random
test_list = random.sample(range(1, 21), 20)
print("Original list:", test_list)
sorted_list = modified_bubble_sort(test_list.copy())
print("Sorted list:", sorted_list)
🔹 Optimized Features:
✔ Introduces a swapped flag to break early if the list is already sorted.
✔ Reduces unnecessary passes, improving best-case performance to O(n).
✔ Still has an average and worst-case time complexity of O(n²).
💡 Key Takeaway: The modified bubble sort improves efficiency for nearly sorted lists but remains inefficient for large datasets.
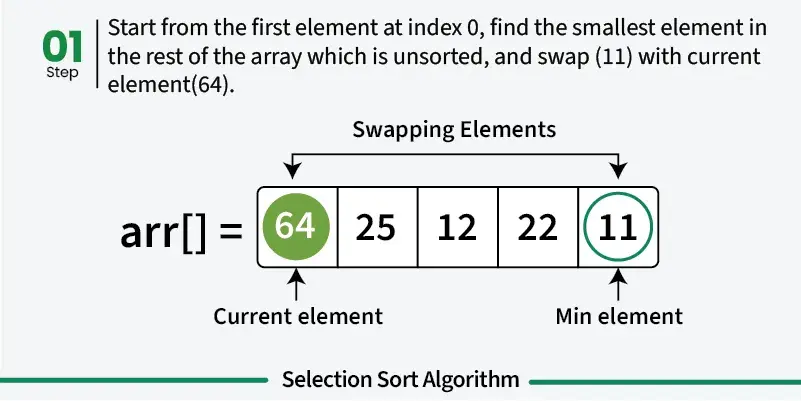
2. Selection Sort with Reverse Order Support
📌 Key Insight: Selection sort is efficient for small datasets and can be easily modified for descending order sorting.
🔹 Code Implementation (Python):
def selectionSort(arr, reverse=False):
n = len(arr)
for i in range(n-1):
min_index = i
for j in range(i+1, n):
if reverse:
if arr[j] > arr[min_index]: # Descending order
min_index = j
else:
if arr[j] < arr[min_index]: # Ascending order
min_index = j
arr[i], arr[min_index] = arr[min_index], arr[i]
return arr
# Example usage
arr = [64, 25, 12, 22, 11]
sorted_arr = selectionSort(arr, reverse=True)
print("Sorted array in descending order:", sorted_arr)
🔹 Optimized Features:
✔ Allows sorting in both ascending and descending order.
✔ Maintains a time complexity of O(n²).
✔ Useful when memory is limited, as it performs sorting in-place.
💡 Best Use Case: Selection sort is ideal for small datasets but not recommended for large-scale sorting due to its quadratic complexity.
3. Comparing Sorting Algorithms: Bubble Sort vs. Selection Sort vs. Insertion Sort
📌 Key Insight: Insertion sort performs better for nearly sorted lists, while selection sort is more consistent in performance.
| Algorithm | Best Case | Average Case | Worst Case | Use Case |
|---|---|---|---|---|
| Bubble Sort (Optimized) | O(n) | O(n²) | O(n²) | Small datasets, nearly sorted lists |
| Selection Sort | O(n²) | O(n²) | O(n²) | Memory-efficient sorting |
| Insertion Sort | O(n) | O(n²) | O(n²) | Best for nearly sorted data |
💡 Strategic Insight: If a dataset is partially sorted, insertion sort is the best choice. However, for completely random data, selection sort may perform more consistently than bubble sort.
4. Practical Applications of Sorting Algorithms
✔ Data Processing: Sorting is crucial for organizing large datasets in databases.
✔ Search Optimization: Sorted arrays enable faster search operations using binary search.
✔ Machine Learning Preprocessing: Feature selection often involves sorting data for ranking purposes.
💡 Best Practice: Choosing the right sorting algorithm depends on data size, memory constraints, and initial order.
Conclusion
Sorting algorithms form the backbone of efficient computing and data manipulation. While optimized bubble sort improves performance for nearly sorted lists, selection sort with reverse support provides a flexible and memory-efficient sorting solution.
Businesses and developers must choose sorting methods based on dataset characteristics, required efficiency, and computational limitations.
📥 Download Full Code (Python): Click Here
Related Computer Science Resources 📚
🔹 Best Sorting Algorithms for Large Datasets
🔹 Time Complexity Explained: Big-O Notation Guide
🔹 Sorting in Python: A Beginner’s Guide
📌 Need expert guidance on algorithm development? 🚀 Our professional writers at Highlander Writers can assist with computer science projects, algorithm analysis, and Python programming tutorials!
Leave a comment
Your email address will not be published. Required fields are marked *